¡Oye! 44+ Listas de Standardabweichung Binomialverteilung Bedeutung: Eigenschaften der binomialverteilung erwartungswert, varianz und standardabweichung.
Standardabweichung Binomialverteilung Bedeutung | Eine stauchung bedeutet, dass der rote graph breiter aussieht als der graph der standardnormalverteilung. Die standardabweichung ist die wurzel aus der varianz Gefragt 26 jan 2014 von gast. Diese ist die wurzel der varianz. Die varianz einer binomialverteilung entspricht dem produkt aus dem erwartungswert und der misserfolgswahrscheinlichkeit (der gegenwahrscheinlichkeit zum erfolg).
Poissonscher grenzwertsatz für negative binomialverteilungen. In dem video geht es um die berechnung von erwartungswert, varianz und der standardabweichung. Die standardabweichung ist ein maß dafür, wie weit die einzelnen zahlen verteilt sind. Es werden am tag durchschnittlich 196 einwandfreie mikrowellen mit einer standardabweichung von 1,98 mikrowellen produziert. Aber allein in kombination mit dem mittelwert ist die standardabweichung bedeutung bereits sehr aufschlussreich, insbesondere bei normal verteilten daten.

Erwartungswert & standardabweichung der binomialverteilung | fundamente der. Für die berechnung der standardabweichung kannst du eine ein fache formel verwenden: Gelegentlich wird die binomialverteilung auch als binominalverteilung bezeichnet. Ist 𝑋 binomialverteilt mit den parametern 𝑛 und 𝑝, so gilt: Die standardabweichung (σ) bestimmt, ob der graph gestaucht oder gestreckt ist. Was beschreibt varianz und standardabweichung bei binomialverteilungen? Sie sind größer oder gleich null und können für binomialverteilte zufallsvariablen wie folgt berechnet werden: Erwartungswert varianz und standardabweichung sind drei werte, die sich für eine binomialverteilung recht zügig berechnen lassen, wenn wir n und p kennen. Wir untersuchen die streuung um den erwartungswert. Die standardabweichung besitzt die gleiche dimensionwie die messwerte der beobachtungsreihe. Standardabweichung um den erwartungswert, binomialverteilung, aufgabenbeispielwenn noch spezielle fragen sind: Oftmals ist auch nach der standardabweichung gefragt. Nimmt die werte an und hat den erwartungswert, so gilt:
Die standardabweichung ist die wurzel aus der varianz Ist 𝑋 binomialverteilt mit den parametern 𝑛 und 𝑝, so gilt: Oftmals ist auch nach der standardabweichung gefragt. Die standardabweichung ist ein maß dafür, wie weit die einzelnen zahlen verteilt sind. Es ist daher wünschenswert, die ursachen der variabilität zu analysieren, um mit dem quadrat der standardabweichung als ein maß für die variabilität umzugehen.
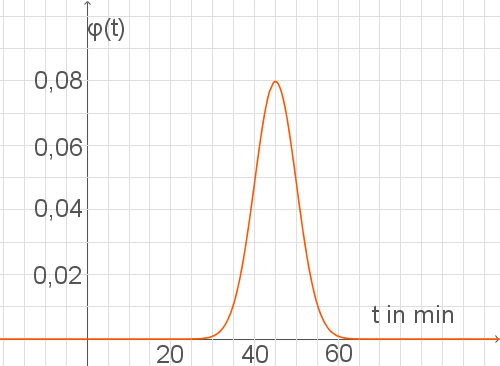
Wenn es zwei unabhängige ursachen der variabilität gibt, die in der lage sind, in einer ansonsten gleichmäßigen populationsverteilung die standardabweichungen and zu produzieren, wird festgestellt, dass die verteilung, wenn beide ursachen zusammen interagieren, eine standardabweichung von, + aufweist. Die varianz einer binomialverteilung entspricht dem produkt aus dem erwartungswert und der misserfolgswahrscheinlichkeit (der gegenwahrscheinlichkeit zum erfolg). Σ = √𝑛⋅𝑝⋅(1−𝑝) aber was hat man davon? Die erste unterrichtseinheit (kenngrößen und wahrscheinlichkeitsverteilung) ist Genauer gesagt, gibt sie an, wie weit die einzelnen messwerte im durchschnitt von dem erwartungswert (mittelwert) entfernt sind. Es ist daher wünschenswert, die ursachen der variabilität zu analysieren, um mit dem quadrat der standardabweichung als ein maß für die variabilität umzugehen. Sie beschreibt die anzahl der erfolge in einer serie von gleichartigen und unabhängigen versuchen, die jeweils genau zwei mögliche ergebnisse haben. Poissonscher grenzwertsatz für negative binomialverteilungen. Die binomialverteilung ist eine der wichtigsten diskreten wahrscheinlichkeitsverteilungen. Wir untersuchen die streuung um den erwartungswert. Die varianz und ihr unterschied zur standardabweichung Analog hierzu definieren wir für wahrscheinlichkeitsverteilungen: Was ist die varianz, was ist die standardabweichung?
Die standardabweichung (σ) bestimmt, ob der graph gestaucht oder gestreckt ist. „sigma) in anwendungen insbesondere für die empirische standardabweichungoft soder sd(für englisch standard Varianz und standardabweichung für binomialverteilungen Erwartungswert & standardabweichung der binomialverteilung | fundamente der. Standardabweichung σ = √n ⋅ p ⋅ (1 _
Ist die streuung groß genug, so lässt sich die entsprechende binomialverteilung brauchbar durch die normalverteilung annähern. Berechnung von erwartungswert, varianz und standardabweichung. Die standardabweichung besitzt die gleiche dimensionwie die messwerte der beobachtungsreihe. Die streuung einer zufallsvariable um ihren erwartungswert wird varianz genannt. Was beschreibt varianz und standardabweichung bei binomialverteilungen? Die varianz und ihr unterschied zur standardabweichung Für statistik im ba sind meist diese beiden verteilungsformen von bedeutung. Wir untersuchen die streuung um den erwartungswert. Die standardabweichung ist ein maß dafür, wie weit die einzelnen zahlen verteilt sind. Aus der beschreibenden statistik ist die varianz, bzw. Die standardabweichung als streumaß bekannt. Nimmt die werte an und hat den erwartungswert, so gilt: Ist p {\displaystyle p} die erfolgswahrscheinlichkeit bei einem versuch und n {\displaystyle n} die anzahl der versuche, dann bezeichnet man mit b {\displaystyle b} die wahrscheinlichkeit.
Eigenschaften der binomialverteilung erwartungswert, varianz und standardabweichung standardabweichung binomialverteilung. Poissonscher grenzwertsatz für negative binomialverteilungen.
Standardabweichung Binomialverteilung Bedeutung! Weitere interessante inhalte zum thema näherung für die binomialverteilung
0 Response to "¡Oye! 44+ Listas de Standardabweichung Binomialverteilung Bedeutung: Eigenschaften der binomialverteilung erwartungswert, varianz und standardabweichung."
Post a Comment